Exercice 24 Durée de vie du muon¶

Quelle sont sa charge et sa masse dans les unités de base du système international ? Comparer cette masse à celle de l’$e^{-}$.
La particularité du $\mu$ est d'être instable et de se désintégrer spontanément suivant le mode :$$\mu^{-}\longrightarrow e^{\pm}+\nu_{\mu}+\overline{\nu_{e}}$$ Quelle doit être la nature de la particule produite (électron/positron) pour que la désintégration soit possible?
Etablir l'équation différentielle donnant la variation $dN\left(t\right)$ d'une population de $N\left(t\right)$ muons au cours d'un temps $dt$.
En déduire l'évolution de $N\left(t\right)$. Tracer l'allure de $N\left(t\right)$.
Pour une décroissance exponentielle, la durée de vie moyenne $\tau$ d'un muon est le temps de décroissance caractéristique de l'exponentielle. Montrer alors que $\tau=\frac{1}{\lambda}$.

En pratique, cette durée de vie moyenne est déterminée par l’expérience. Les premières ont été menées à la fin des années 30 et tout début des années 40 mais ne sont pas facilement exploitables. On donne ci-dessous une courbe obtenue lors d’une expérience similaire réalisée en 1963.

$schéma de principe de l’arrêt d’un muon dans un détecteur cubique au temps $t_{1}$ (à gauche) et de sa désintégration au temps $t_{2}$ (à droite).$

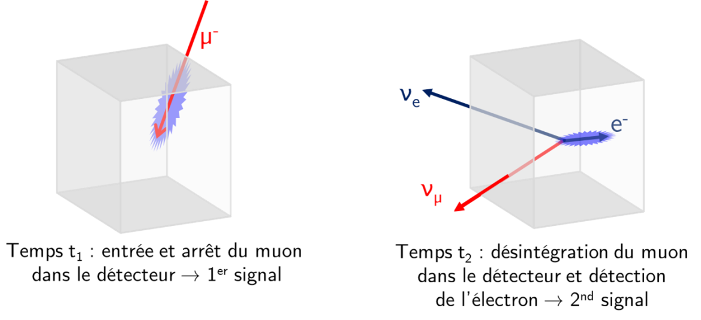
Les muons sont arrêtés dans un détecteur (ce qui produit un 1er signal) qui est sensible à leur désintégration (2nd signal). En mesurant systématiquement le temps écoulé entre les 2 signaux, on peut déduire la fraction de la population de muons restant au bout d’un temps t après leur arrêt.

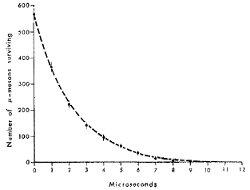
Il est toutefois plus facile de déterminer la durée de vie en représentant non pas le nombre de muons non-désintégrés mais son logarithme népérien en fonction du temps comme ci-dessous.
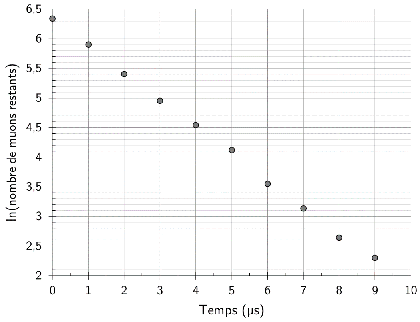
Donner l’expression attendue pour cette courbe et par ajustement graphique, en déduire la durée de vie moyenne $\tau$.

Les muons dans les rayons cosmiques : Les muons sont produits essentiellement suite aux interactions de protons de haute énergie venant du Soleil avec les nucléons des noyaux de la haute atmosphère qui produisent des pions (assemblage de quarks et antiquarks u et d). Ces pions se désintègrent (dans $99,99\%$ des cas) en muons suivant les désintégrations suivantes :

$$ \begin{array}{ccccc} \pi^{-} & \longrightarrow & \mu^{-} & + & \overline{\nu_{\mu}}\\ \pi^{+} & \longrightarrow & \mu^{+} & + & \nu_{\mu} \end{array} $$

Et enfin, les muons subissent une désintégration en $e^{\pm}$ comme vu ci-dessus.

Les pions ayant une durée de vie brève (environ 100 fois plus courte que celle des muons), les muons sont produits essentiellement dans la stratosphère (>15km d'altitude) et ont des vitesses proches de la vitesse $c$ de la lumière dans le vide. La majeure partie se désintègre avant d'arriver au sol mais on peut encore observer un flux conséquent à la surface de La Terre. Ceci permet une autre évaluation de leur durée de vie en faisant des expériences à différentes altitudes. C'est ce qui a été réalisé dans l'expérience de 1963 où deux prises de mesures ont été réalisées : l'une proche du sommet du Mont Washington (New Hampshire), l'autre au MIT à Cambridge (Massachusetts) . Les résultats sont présentés dans le tableau ci-dessous.

Lieu Altitude (m) Nombre de muons détectés par heure

Mont Washington (NH) $1910$ $563\pm10$

Cambridge (MA) $3$ $408\pm9$
En considérant que les muons se déplacent à une vitesse $v=0,995c$, calculer le temps $\Delta t$ qu’il leur faut pour parcourir les $\Delta h=1907m$ séparant les altitudes des deux points de mesure.
En utilisant la durée de vie moyenne calculée précédemment, en déduire le rapport attendu entre les mesures réalisées aux deux altitudes.
Quel est le rapport obtenu expérimentalement (on donnera le résultat assorti de son incertitude) ?

Cette différence s'explique par la très grande vitesse $v$ des muons. La physique newtonienne n'est plus valable lorsque la condition $v\ll c$ n'est pas respectée. Il faut alors utiliser la relativité restreinte qui prédit en particulier la dilatation des temps (cf. cours de relativité en L3 physique). Le temps propre de la particule se voit dilaté dans un référentiel se mouvant à une vitesse $v$ par rapport à elle par un rapport :

$$\gamma=\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$$
Calculer la durée $\Delta t_{\mu}$ apparente pour les muons du trajet de longueur $\Delta h$.
En déduire quel est le rapport réel entre le flux au sommet du Mt Washington et le flux au MIT ?

Le $\mu^{-}$ a la même charge électrique que l'électron soit $e=1.6021766208\times10^{-19}A.s$,

la masse du muon en $kg$ est donnée par $m_{\mu}=105.66\times10^{6}\times1.6021766208\times10^{-19}/(299792458)^{2}=1,88\times10^{-28}kg$.

On a $$\frac{m_{\mu}}{m_{e}}=\frac{105,66}{0,511}=206,77$$
Lors de la désintégration, la charge électrique totale doit être conservée, or les neutrinos sont neutres.

Donc $\mu^{-}$ se désintégre en un électron $e^{-}$, l'équation de la désintégration est donc : $$\mu^{-}\longrightarrow e^{-}+\nu_{\mu}+\overline{\nu_{e}}$$
Stabilité ou instabilité d’une particule élémentaire

Une particule élémentaire est stable s’il n’existe pas dans sa famille une autre particule élémentaire de plus faible masse vers laquelle elle peut se désintégrer spontanément en libérant de l’énergie. En effet, sans apport d’énergie extérieur, la conservation de l’énergie implique qu’une particule plus légère ne peut pas se désintégrer en une particule plus lourde. Ainsi, le muon est instable car il peut se désintégrer en électron par le biais de l’interaction faible. L’électron est stable car il n’existe pas une particule chargée plus légère que lui dans la famille des leptons.

Probabilité de désintégration d’un muon

Chaque muon au repos a une probabilité constante $\lambda$ de se désintégrer par unité de temps. Un $\mu^{-}$ n’a donc pas plus de chance de se désintégrer 1 microseconde ($\mu s$) ou $10 \mu s$ après sa création… Cela signifie que tous les muons n’ont pas la même durée de vie mais que l’on peut prévoir quelle chance un muon détecté à un instant a de s’être désintégré ou non au bout au temps . Si l’on raisonne sur toute une population de muons, on peut ainsi prévoir quelle fraction de cette population se sera désintégrée ou sera encore présente. L’origine du temps choisie n’a pas d’importance, seul $\delta t=t-t_0$ importe puisque la probabilité de désintégration par unité de temps est constante.

Le nombre de muons se désintégrant par unité de temps est proportionnel au nombre de muons à l'instant considéré, on a donc $\frac{dN\left(t\right)}{dt}=-\lambda N\left(t\right)$ où $\lambda$ est la probabilité de désintégration par unité de temps.

Considérons 9 muons et observons leur désintégration

Le graphe de gauche montre les muons, celui de droite représente le nombre de muons survivant (en orange) et le compare à la fameuse exponentielle décroissante en (en rouge)

Considérons 25 muons et observons leur désintégration

Considérons 121 muons et observons leur désintégration

Considérons 441 muons et observons leur désintégration

Considérons 1681 muons et observons leur désintégration

Aux fluctuations statistiques près, plus importantes lorsque le nombre de particules est faible, on retombe toujours sur la même courbe...
On a alors en intégrant l'équation : $N\left(t\right)=N_{0}e^{-\lambda t}$ si $N_{0}$ est le nombre de muons à l'instant $t=0$.
A partir de l’expression de $N\left(t\right)$, on peut introduire un temps caractéristique de désintégration, égal à l’inverse de la constante de désintégration $\lambda$, et qui correspond à la durée de vie moyenne $\tau$ d’un muon au repos.
La droite a pour équation $\ln N\left(t\right)=\ln N_{0}-\lambda t$, en traçant la meilleure droite et en prenant l'opposé du coefficient directeur de la droite, on arrive à $\lambda=4,55.10^{5}s^{-1}$, cela correspond à une durée de vie $\tau=2,2\mu s$ (attention, $\tau$ et la demi-vie diffèrent d'un facteur $\ln2$).
On a $\Delta t=\frac{\Delta h}{v}=\frac{1907}{0,995\times3.10^{8}}=6,39\mu s$.
On a $\frac{N\left(t_{0}+\Delta t\right)}{N\left(t_{0}\right)}=e^{-\lambda\Delta t}=e^{-\frac{6,39}{2,2}}=5,5\%$
Expérimentalement, on a $\frac{N\left(t_{0}+\Delta t\right)}{N\left(t_{0}\right)}=\frac{408}{563}=0,725$ et $\delta\frac{N\left(t_{0}+\Delta t\right)}{N\left(t_{0}\right)}=\sqrt{\left(\delta N\left(t_{0}+\Delta t\right)\right)^{2}+\left(\delta N\left(t_{0}\right)\right)^{2}}=\sqrt{10^{2}+9^{2}}=13$ donc $\frac{N\left(t_{0}+\Delta t\right)}{N\left(t_{0}\right)}=72\pm13\%$
Le temps propre des muons est plus court d’un facteur $\sqrt{1-\left(\frac{v}{c}\right)^{2}}=\sqrt{1-0,995^{2}}=9,987.10^{-2}$, ce qui correspond à un temps de vol propre pour parcourir $\Delta h$ de $\Delta t_{\mu}=6,39\times9,987.10^{-2}\mu s=0,638\mu s$.
On a alors $\frac{N\left(t_{0}+\Delta t\right)}{N\left(t_{0}\right)}=e^{-\lambda\Delta t}=e^{-\frac{0,638}{2,2}}=74,8\%$

Le graphe de gauche montre l'état (désintégré ou pas) des muons au repos, celui du centre montre l'état des muons du rayonnement cosmique (relativistes), celui de droite représente le nombre de muons survivants (en orange pour les muons au repos, en violet pour les muons relativistes du rayonnement cosmique) et le compare à la fameuse exponentielle décroissante en (en rouge) donnée pour les muons au repos.

Considérons 1681 muons et observons leur désintégration

Outils de simulation¶

Voici pour l'exemple, un des bouts de code python qui ont permis de produire certaines animations.

from pylab import *
from random import random
import matplotlib.animation
import matplotlib.colors as colors

rcParams['animation.embed_limit'] = 200

class muon():
    def __init__(self):
        self.duree_vie = 2.2e-6
        self.demi_vie = self.duree_vie*log(2) 
        self.lamda = 1/self.duree_vie
        self.alive = True
        self.color = "lime"
    def test(self,dt):
        if(self.alive):
            desproba = self.lamda*dt 
            self.alive = (random()>desproba)
            if (not self.alive):
                return True
        return False
    def alpha(self):
        return 1 if self.alive else 0.2
    def lamda(self):
        return self.lamda

t_ini = 0
t_fin = 1e-5
dt = 1e-8
t_tab = arange(t_ini,t_fin,dt)

scatter([],[])

tab_m = []

nmu_x = 1
nmu_y = 1

nx = linspace(-nmu_x,nmu_x,2*nmu_x+1) # nmu_x = 1 -> 3 valeurs -1 0 1
ny = linspace(-nmu_y,nmu_y,2*nmu_y+1) # nmu_y = 1 -> 3 valeurs -1 0 1

X,Y = meshgrid(nx,ny) # pour nmu_x=nmu_y=1 on construit 3x3=9 couples de positions pour les muons

nmu = nmu_0 =  len(nx)*len(ny)
n_mu = array([])
for i in range(len(nx)*len(ny)):
    tab_m.append(muon())
n_mu_th = nmu_0*exp(-muon().lamda*t_tab)
status = []
    
for t in t_tab:
    stat = []
    for i,m in enumerate(tab_m):
        stat.append(colors.to_rgba("forestgreen",m.alpha()))
        if(m.test(dt)):
#            print(i,'->',t)
             nmu=nmu-1
    n_mu = append(n_mu,nmu)        
    status.append(stat)
    
fig,ax = subplots(1,2,figsize=(16,4))
g1 = ax[0].scatter(X,Y,marker='o',label="muons",s=100)
p2, = ax[1].plot([],[],'-',color='red',label="Nombre de muons (théorique)")
p1, = ax[1].plot([],[],'o',color='orange',label="Nombre de muons (simulation)",ms=2)
t1 = ax[1].text(0.8*t_fin,0.5*nmu_0,'')
ax[0].tick_params(axis='both',          # changes apply to the x-axis
                      which='both',      # both major and minor ticks are affected
                      bottom='off',      # ticks along the bottom edge are off
                      top='off',         # ticks along the top edge are off
                      labelbottom='off',
                      left='off',      # ticks along the bottom edge are off
                      right='off',         # ticks along the top edge are off
                      labelleft='off')
ax[0].set_title("Muons au repos")
ax[1].set_xlabel("t [s]")
ax[1].set_ylabel("$N_\mu$")
ax[1].set_xlim([t_ini,t_fin])
ax[1].set_ylim([0,nmu_0])
ax[1].set_title("Nombre de muons survivants")
ax[1].legend(loc="upper right")

def animate(i):
    g1.set_color(status[i])
    p2.set_data(t_tab[:i],n_mu_th[:i])
    p1.set_data(t_tab[:i],n_mu[:i])
    t1.set_text("t = %5.2es"%(t_tab[i]))

# Set up formatting for the movie files
Writer = matplotlib.animation.writers['ffmpeg']
writer = Writer(fps=15, metadata=dict(artist='Me'), bitrate=1800)    
    
ani = matplotlib.animation.FuncAnimation(fig, animate, frames=len(t_tab))
#ani.save('muons_%d.mp4'%(len(nx)*len(ny)), writer=writer)


from IPython.display import HTML
HTML(ani.to_jshtml())

Lieu	Altitude (m)	Nombre de muons détectés par heure
Mont Washington (NH)	$1910$	$563\pm10$
Cambridge (MA)	$3$	$408\pm9$