Exercice 23 Radioactivité $\beta$

$$_{83}^{210}Bi\longrightarrow_{84}^{210}Po+\beta$$

On donne les énergies de masse suivantes :

	noyau $_{83}^{210}Bi$	noyau $_{84}^{210}Po$	$e^{-}$
Energie de masse (MeV)	$195556,5341$	$195554,8618$	$0,511$
masse (u)	$209,9385869\thinspace(16)$	$209,9367917\thinspace(13)$	$5,486\times10^{-4}$

1. Déterminez la composition en protons et neutrons de la particule $\beta$ ainsi que sa charge électrique. Quelle est alors sa nature ?

2. En calculant la variation de masse $\Delta m$ puis la variation d’énergie de masse $\Delta Em$ (comme pour l'exercice précédent), on obtient une valeur de $1,161\ MeV$. On s’attend au même scénario que la radioactivité $\alpha$ : la particule bêta et le noyau se partagent l’énergie cinétique et sont émis en direction opposée (figure ci-dessous).

   

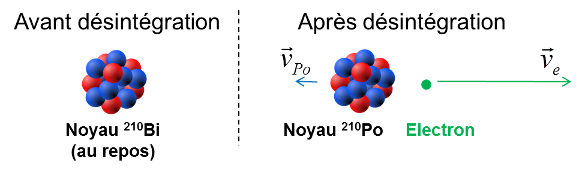
   Pourquoi l’électron va-t-il emporter en pratique toute l’énergie libérée ?

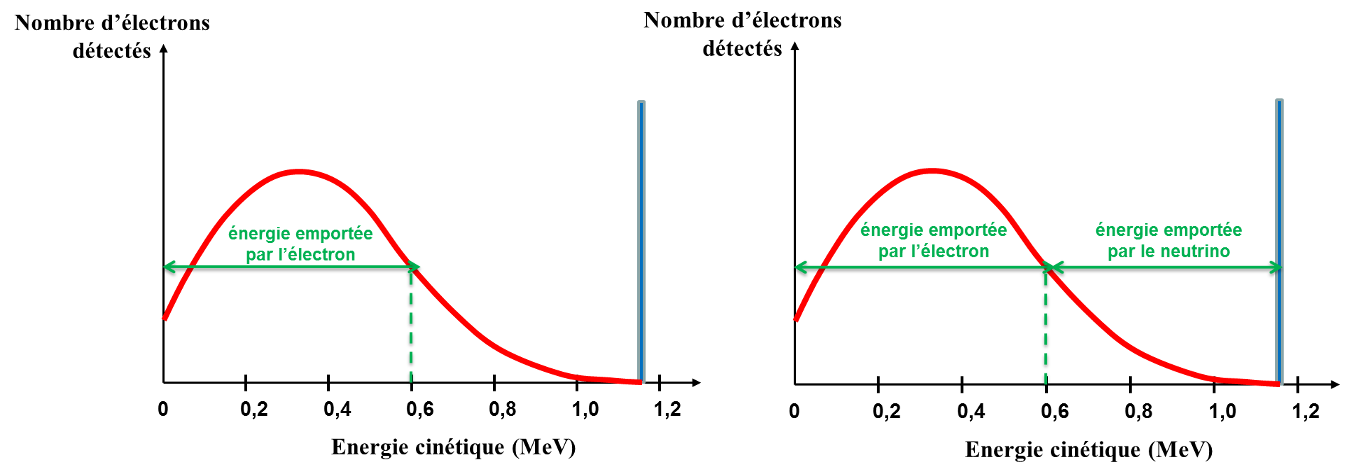
   On attend donc que les électrons bêta déposent une énergie de $1,161\ MeV$ à chaque fois qu’ils sont arrêtés dans le détecteur. En réalité, on observe un spectre en énergie des électrons continu entre $0$ et l’énergie de $1,161\ MeV$ (figure ci-dessous à droite) et non pas le spectre attendu avec un pic mono-énergétique, similaire à la radioactivité alpha.

   

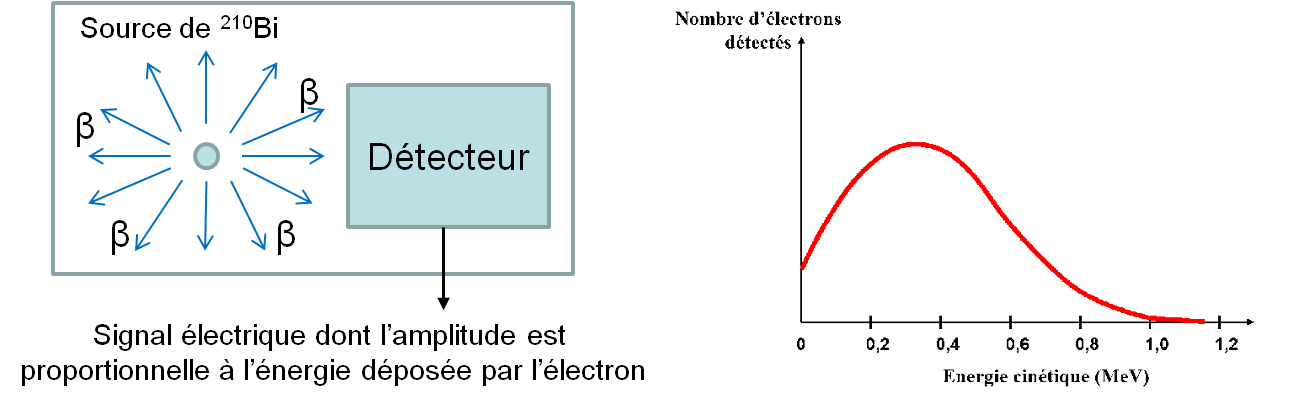
   Comment interpréter ce résultat?

3. Le noyau de bismuth est au repos. Comment se fait alors le partage de l’énergie dans la désintégration ? Ecrire alors la conservation de l’énergie.

4. Ecrire également la conservation de l’impulsion. Montrer que l’on a 3 inconnues et seulement 2 équations. Qu’est-ce que cela signifie pour le nombre de solutions ?

5. Dans le cas où l’électron est produit avec une énergie cinétique de $0,60\ MeV$, que vaut celle du neutrino ? Faire apparaître la part en énergie de chacun sur la figure ci-dessous. Dans le cas l’électron possède une énergie cinétique nulle, que vaut celle du neutrino ?

6. En étudiant l’insert dans la figure ci-dessous (zoom sur la partie à plus haute énergie de la distribution) ainsi que les masses données dans le tableau, donner une valeur majorante de la masse du neutrino avec l’incertitude associée. Peut-on dire qu’il a une masse nulle ? Ou une masse inférieure à une certaine valeur ?

   

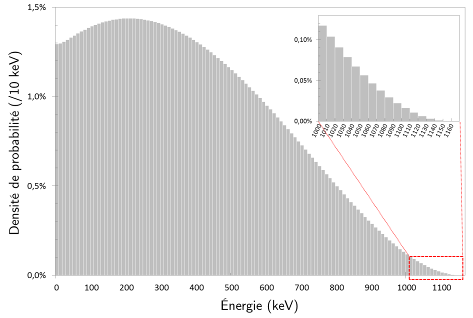
1. On utilise les lois de conservation :

   • Du nombre de nucléons $A$ : $A(\beta)=A(Bi)-A(Po)=210-210=0$. La particule bêta n’est pas un nucléon

   • De la charge électrique: $Z(\beta)=Z(Bi)-Z(Po)=83-84=-1$. La particule $\beta$ possède une charge électrique négative et égale à $–e$. Il s’agit donc d’un électron.

   Remarques :

   • Dès 1900, H. Becquerel identifie cette particule à l’électron découvert 3 ans plus tôt par J. J. Thomson.

   • Il s’agit au niveau des nucléons de la transformation d’un neutron en proton.

   • Le neutron n’étant découvert qu’en 1932, les physiciens pensaient que l’électron préexistait dans le noyau atomique et qu’il était alors éjecté. On sait aujourd’hui que l’électron est créé au moment de la désintégration bêta du fait de l’énergie disponible qui créé sa masse.

2. En comparant la masse de l’électron et celle de la particule alpha de l'exercice précédent, on constate que $m_{e}\sim\frac{1}{7300}m_{\alpha}$. Or, la particule alpha était déjà très légère devant le noyau et emportait malgré tout $98\%$ de l’énergie cinétique.

   Donc ici, $m_{e}\ll m(Po)$, d’où $E_{c}(e)\gg E_{c}(Po)$. L’électron emporte donc $\sim100\%$ de l’énergie cinétique d’où $E_{c}(e)=1,161\ MeV$.

   Comment interpréter le spectre continu observé?

   Devant ce résultat inattendu, les physiciens se sont interrogés :

   • Faut-il remettre en cause le principe de conservation de l’énergie au niveau microscopique/subatomique ?

   • Y-a-t-il « autre chose » émis dans la désintégration bêta que l’on ne voit pas et qui emporte une partie de l’énergie ?

   La conservation de l’énergie et de l’impulsion étant des piliers de la physique, il était plus « logique » de penser qu’une autre particule non détectée était émise. On va voir pourquoi par la suite.

   En 1930, Wolfgang Pauli propose l’existence d’une nouvelle particule, le neutrino (notée $\nu$) pour expliquer le spectre en énergie continu des électrons issus de la désintégration . Lorsqu’il a réalisé la difficulté de pouvoir observer un jour le neutrino, il a déclaré par la suite : « J'ai fait une chose terrible : j'ai postulé l'existence d'une particule que l'on ne peut pas détecter. »

   Dans notre exemple, la désintégration s’écrirait alors :$$_{83}^{210}Bi\longrightarrow_{84}^{210}Po+e^{-}+\overline{\nu}_{e}$$

   

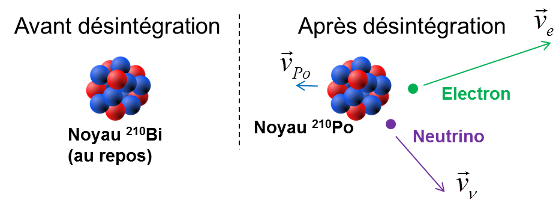
3. L’énergie de masse se transforme en énergie cinétique pour le noyau, pour l’électron et pour le neutrino. Comme on a montré à la question b) que l’énergie cinétique du noyau était négligeable car trop lourd, on a alors : $\Delta E_{m}=E_{c}\left(e\right)+E_{c}\left(\nu\right)$

4. Comme le noyau de bismuth est au repos, sa quantité de mouvement est nulle. Donc : $$\vec{P}_{Po}+\vec{P}_{e}+\vec{P}_{\nu}=\vec{0}$$

   Dans ce cas, la quantité de mouvement $P_{Po}$ du noyau de Polonium n’est pas négligeable (car c’est $mv$ alors que l’énergie cinétique est $\frac{1}{2}mv^{2}$ avec un terme $v^{2}$ donc un terme au $2^{\grave{e}me}$ ordre). Donc on a $3$ inconnues ($P_{Po}$, $E_{c}(e)$ et $E_{c}(v)$) et seulement $2$ équations. Cela conduit mathématiquement à une infinité de solutions. Physiquement, cela signifie que l’électron et le neutrino se partagent l’énergie d’une infinité de manières !

5. $\ $

   

   On sait que la variation d’énergie de masse vaut $1,161\ MeV$. D’après la conservation de l’énergie, on a $\Delta E_{m}=E_{c}\left(e\right)+E_{c}\left(\nu\right)$ donc $E_{c}\left(\nu\right)=\Delta E_{m}-E_{c}\left(e\right)$

   Quand $E_{c}(e)=0,6\ MeV$, le neutrino a emporté $1,161-0,6=0,561\ MeV$. On peut donc compléter la figure ci-dessus (à droite) pour montrer l’énergie complémentaire emportée par le neutrino.

   Quand $E_{c}(e)=0\ MeV$, le neutrino a emporté $1,161-0=1,161\ MeV$.

6. Le calcul de l’énergie $\Delta E_{m}$ libérée dans la transition donne : $\Delta E_{m}=\left(M_{^{210}Bi}-M_{^{210}Po}-m_{e}\right)c^{2}=209,9385869-209,9367917-5,486\times10^{-4}=0.00125u=1,1613\ MeV$

   Les incertitudes n’étant données dans la table que pour les masses en u, on fait le calcul avec celles-ci puis on convertit de u en MeV avec la valeur de l’unité de masse atomique ($1u=931,494028\ MeV.c^{-2}$ pour trouver le $\delta\Delta E_{m}$ : $\delta\Delta E_{m}=\sqrt{\left(\Delta M_{^{210}Bi}\right)^{2}-\left(\Delta M_{^{210}Po}\right)^{2}}=931,494028\times\sqrt{\left(16.10^{-7}\right)^{2}+\left(13.10^{-7}\right)^{2}}=0.0019\ MeV$.

   (note : on a ici négligé l’incertitude introduite par la conversion en MeV ce qui ce justifie car l’incertitude relative sur la valeur de l’unité de masse atomique en MeV est de l’ordre de $10^{-8}$). On a donc une valeur finale de $\Delta E_{m}=1,1613(19)\ MeV$.

   Si l’on appelle $E_{ep}$ l’énergie maximale (end point) du spectre $\beta$ , la masse du neutrino est donnée par $m_{\nu}=\Delta E_{m}-E_{ep}\pm\sqrt{\left(\delta\Delta E_{m}\right)^{2}+\left(\Delta E_{ep}\right)^{2}}$ .

   En réalité, il est difficile de mesurer précisément $E_{ep}$ car la statistique est très faible au bout du spectre. On peut tout au plus donner une valeur majorant $E_{ep}>1155\pm5\ keV$.

   On obtient donc $m_{\nu}<1,1613-1,155\pm\sqrt{0,0019^{2}+0,005^{2}}\ MeV$ Soit finalement $m_{\nu}=6,3\pm5,4\ keV$.

   Cette méthode permet donc d’affirmer que le neutrino a une masse inférieure à $12\ keV$.