Pour aller plus loin (Vers l'infini et au-delà...)¶
“Il y a autant de molécules d'eau dans 10 gouttes d'eau que d'étoiles dans l'Univers"¶
L'image de gauche représente quelques gouttes déposées sur une vitre, celle de droite une portion de l'univers. Les points brillants sont des galaxies.
Quel est le nombre d'étoiles dans l'Univers?¶
On souhaite tout d'abord avoir une estimation du nombre d'étoile dans la Voie Lactée.
Remarque : notre galaxie se nomme Voie Lactée ou Galaxie (avec une majuscule). Pour estimer la masse de notre galaxie, on peut appliquer la relation de Kepler généralisée.
Montrer que la relation de Kepler généralisée peut se mettre sous la forme :$$\frac{T^{2}}{a^{3}}=\frac{K}{M_{G}}$$ où $T$ est la période orbitale d'un corps autour du centre galactique, $a$ le rayon de cette orbite, $M_{G}$ la masse de la galaxie et $K$ une constante à définir.
Sachant que le Soleil tourne autour du centre de la Galaxie en $220\times10^{6}\thinspace\text{ans}$ sur une orbite de $26000\ \text{a.l.}$. de rayon, calculer la masse de la Galaxie (en masse solaire).
Est-ce bien la masse de la Galaxie que l'on calcule par cette méthode ?
Quel est le nombre de galaxies dans l'Univers ? Pour estimer ce nombre, on s'appuie par exemple sur les photographies de champ profond obtenues par le télescope spatial Hubble. Le terme de profond est utilisé ici au sens de lointain dans l'espace et dans le temps.
Image 1: Le “Hubble Ultra Deep Field $2014$” (Le champ ultra-profond de Hubble $2014$). Photographie composite constituée d'images prises par le télescope spatial Hubble dans l'UV, le visible et l'infrarouge. La lumière de certaines galaxies présentes sur cette image a été émise quelques centaines de millions d'années après le Big Bang (il y a donc plus de $13$ milliards d'années). Il a fallu un total de $600\ \text{h}$ d'exposition pour obtenir cette photographie (à partir de $841$ orbites du télescope entre $2002$ et $2012$).D'après le site Wikipedia, la taille apparente de la portion de la sphère céleste photographiée sur cette figure correspond à peu près à celle d'un carré de $1mm$ de coté vu à une distance de $1,4\ \text{m}$. Calculer la taille apparente approximative de cette portion de sphère céleste en minute d'arc.
En fait, la taille apparente de la portion de la sphère céleste visible sur cette photographie est de $2,4'$. Quel est l'angle solide de la sphère céleste visible (exprimée en minute d'arc carrée) ?
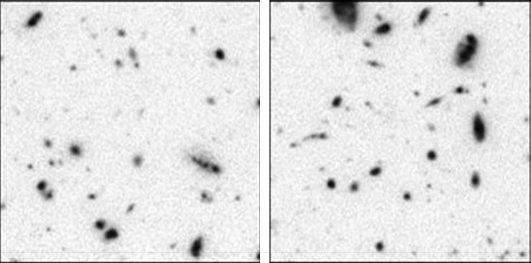
Sachant que chaque tache est une galaxie (!), on peut compter (même grossièrement) le nombre de galaxies visibles sur cette image. Pour cela, compter le nombre de galaxies dans les deux portions suivantes (chaque portion correspond à un carré blanc de l'image, les couleurs sont inversées et les images en noir et blanc pour faciliter le comptage). En déduire ensuite le nombre de galaxies sur l'ensemble de l'image.
Une analyse plus poussée de l'image 1 donne un nombre d'environ $10000$ galaxies. Quel est le nombre de galaxies dans notre Univers ? et le nombre d'étoiles ?
Nombre d'étoiles dans la voie Lactée
La loi de Kepler généralisée pour un corps (une étoile par exemple) de masse $m$ en orbite autour du centre de la Galaxie de masse $M_{G}$ est donnée par :$$\frac{T^{2}}{a^{3}}=\frac{4\pi^{2}}{{\cal G}\left(M_{G}+m\right)}$$ Il est tout à fait légitime de considérer que la masse $m$ est négligeable devant $M_{G}$, on a donc $$\frac{T^{2}}{a^{3}}=\frac{4\pi^{2}}{{\cal G}M_{G}}\Rightarrow\frac{T^{2}}{a^{3}}=\frac{K}{M_{G}}$$ avec $K=\frac{4\pi^{2}}{{\cal G}}=\frac{4\pi^{2}}{6,67\times10^{-11}}=5,92\times10^{11}\ kg^{2}.m^{-2}.N^{-1}$
Une année lumière vaut $1\ \text{a.l.}=365,25\times86400\times299792458=9,4607\times10^{15}\ \text{m}$
Donc le centre galactique se trouve à $a=26000\times9,4607\times10^{15}=2,4598\times10^{20}\ \text{m}=2,4598\times10^{17}\ \text{km}$
On a alors $M_{G}=\frac{Ka^{3}}{T^{2}}=\frac{5,92\times10^{11}\times\left(2,4598\times10^{20}\right)^{3}}{\left(22\text{0}\times10^{6}\times86400\times365,25\right)^{2}}=1,8275\times10^{41}\ \text{kg}$
Soit $M_{G}=\frac{1,8275\times10^{41}}{1,99\times10^{30}}=9,184\times10^{10}\ M_{\odot}$.
La masse de la Galaxie est environ de $100$ milliards de masses solaires. C'est pourquoi, on dit que la Galaxi contient environ $100$ milliards d'étoiles (en estimant qu'en moyenne elles ont toutes la masse du Soleil).
En réalité, ce calcul ne représente que le calcul du nombre d'étoiles présentes à l'intérieur de l'orbite du Soleil. L'ensemble des étoiles à l'extérieur de l'orbite du Soleil ayant une contribution nulle en terme de gravitation ressentie par le Soleil.
Remarque : on considère ici que toute la masse de la Galaxie est de la masse stellaire, pourtant une partie de cette masse se retrouve dans les nuages de gaz et surtout!!! dans la matière noire.
Nombre de galaxies dans l'Univers
Si $D$ est la dimension de l'objet et d sa distance à l'observateur, la taille angulaire de l'objet est alors donnée par $\alpha\approx\frac{D}{d}$,
donc ici, on a $\alpha\approx\frac{1}{1400}=7,143\times10^{-4}rad=7,143\times10^{-4}\times\frac{180}{\pi}deg=4\times10^{-2}\ \text{deg}=7,143\times10^{-4}\times\frac{180}{\pi}\times60arcmin=2,45'$
Remarque : La taille angulaire de la Lune (ainsi que celle du Soleil d'où les éclipses totales de Soleil) est d'environ $30'$.
L'angle solide visible est simplement le carré de $2,4'$, soit $\Omega=5,76arcmin^{2}$.
On compte environ $40$ et $50$ galaxies sur ces images. Cela fait une moyenne de $45$ galaxies par carré et comme il y a $10\times11=110\ \text{carrés}$ dans l'image, il y a donc environ $5000$ galaxies.
On fait l'hypothèse que la distribution des galaxies dans l'Univers est à peu près homogène sur la sphére céleste (il y a en moyenne le même nombre de galaxies quelle que soit la région de même surface sur la sphère céleste).
L'angle solide de la sphère céleste est $\Omega_{S}=4\pi\thinspace\text{sr}$, soit $12,566$ radian carré. Il faut transformer cet angle solide en minutes d'arc carré. On a $\Omega_{S}=4\pi\left(\frac{180}{\pi}\times60\right)^{2}=1,485\times10^{8}$ minutes d'arc carré.
Le nombre de galaxies dans l'Univers est donc d'environ $N=10000\times\frac{\Omega_{S}}{\Omega}=258\times10^{9}$.
Conclusion, il y a environ $260$ milliards de galaxies dans l'Univers,
si on fait l'hypothèse qu'en moyenne une galaxie contient autant d'étoiles que la voie Lactée, on obtient $N_{\star}=260\times10^{9}\times10^{11}\approx2\times10^{22}$ étoiles dans l'Univers (c'est l'ordre de grandeur qui est important).
Et pour les molécules d'eau dans 10 gouttes?¶
Calculons le volume d'une goutte d'eau
Trois approches...
• On peut faire une estimation visuelle du volume de la goutte,
on la modélise par une sphère de $5\ \text{mm}$ de diamètre, son volume est alors $V=\frac{4\pi}{3}\left(\frac{D}{2}\right)^{3}=\frac{\pi D^{3}}{6}=\frac{\pi\times\left(5\times10^{-3}\right)^{3}}{6}=6,54\times10^{8}\ \text{m}^{3}=0,0654\ \text{ml}$. Donc $V_{10}=0,654\ \text{ml}$.
• On peut faire l'expérience,
prenons une très petite seringue $1\ \text{ml}$, remplissons la d'eau, comptons $10$ gouttes, on regarde de combien le piston s'est déplacé. On trouve $V_{10}=0,5\ \text{ml}$.
• On peut chercher une référence bibliographique
une goutte est une unité de volume définie (on cherche dans Wikipedia...), elle vaut $V=0,05\ \text{ml}$, soit $V_{10}=0,5\ \text{ml}$.
On prendra donc $V_{10}=0,5\ \text{ml}=5\times10^{-7}\text{m}^{3}$ (c'est un choix, on aurait aussi bien pu prendre $V_{10}=0,654\ \text{ml}$, seuls les ordres de grandeur nous intéressent).
Calculons la masse d'eau liquide dans dix gouttes d'eau
La masse volumique de l'eau est dans les conditions normales de pression et de température $\rho=1\ g.cm^{-3}=10^{3}\ kg.m^{-3}$. La masse de 10 gouttes d'eau est alors $M_{10}=\rho\times V_{10}=10^{3}\times5\times10^{-7}=5\times10^{-4}\ \text{kg}=0,5\ \text{g}$
Nombre de moles dans 10 gouttes d'eau
La masse molaire de l'eau est $m=18\ \text{g.mol}^{-1}$, donc dans $10$ gouttes d'eau, on a $N=\frac{M_{10}}{m}=\frac{0,5}{18}=0,028\ \text{mol}$
Nombre de molécules dans $10$ gouttes d'eau $$n=N\times{\cal N}_{A}=0,028\times6,02\times10^{23}=1,67\times10^{22}$$
Il y a bien autant d'étoiles dans l'Univers que de molécules dans dix gouttes d'eau